Machine Learning Engineer Nanodegree

Algorithms and Techniques

Convolutional Neural Network (ConvNet) as classifier. The network has several parameters that needs to be tuned, including number of epochs, batch size, learning rate, max pool layers and dropout layers. This technique and its parameters are discussed above.

The ConvNet is trained using back-propagation to learn the weight parameters, these weights are used to activate neurons. The main difference of the ConvNet with respect to a regular neural network is that it is specifically designed to recognize visual patterns directly from the image pixels [4].

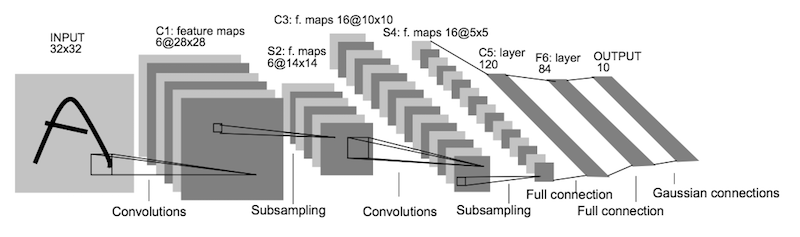alt text Figure-7 Source: Yan LeCun

The figure above shows the LeNet-5 architecture that is intended to be used in this project as the baseline model. The next paragraphs explain how this neural network architecture works when it receives the image and how the image is processed through the network until the output.

Layer name Size Channels
Input 32x32 1
Convolution 1 (C1) 28x28 6
Sub-sampling 14x14 6
Convolution 2 (C2) 10x10 16
Sub-sampling 5x5 16
Fully connect (FC1) 120 -
Fully connect (FC2) 84 -
Output 10 -
Table-1 LeNet5 architecture

The table above denotes the architecture of LeNet-5, the input layer is an image. In this example it is represented as digits comprising images of 32x32 pixels. Here it can be assumed that the image is grayscale such that it has one channel. The dataset of this project are images with 3 channels of color space, for example, Red, Green and Blue.

The first Convolution layer (C1) it is made by applying a convolution that basically scans the image with a patch of smaller size, in this case the patch is 5x5 pixels in size and applying an activation function on it. This patch is applied over the image horizontally and vertically. Once this process finishes, the result will be an image of 28x28. This process will happen six times building up the first convolution layer for the given image. Finally the dimensions of the (C1) layer will be 6@(channels)28x28. This layer represents the automatic extraction of features from the image that was fed into the network.

The second layer is a sub-sampling (S2) that will have the same number of channels as the layer before and the features will be reduced by half, ending with dimensions 6@14x14. This means that a given image after passing the (C1) will end up in (S2) with size of 14x14 pixels and 6 transformations that came from the (C1) layer. The sub-sampling uses a function that is applied together with a patch, in this case the patch size is 2x2 and the function could be a Max function, for example, when you apply a Max function with patch size 2x2 to an image of 28x28 pixels, every patch will choose one pixel with the max value. This process applied to a 28x28 image will occur 196 times and returns an output of size 14x14. This kind of layer aims to reduce the space of feature while retaining the relevant features.

The third layer (C3) it is a convolution similar to the first (C1) but with size of 16@10x10 as a result of applying a patch of size 5x5 pixels. Fourth layer (S4) same as (S2) at this point applied to (C3) ending with size of 16@5x5.

Finally this network has two fully connected layers (FC5), its input is an unrolled version of layer (S4) which is a vector of 400 features (16x5x5) and its output is a vector of 100 features. Next, the sixth layer (FC6) receives as input a vector of 100 features and returns a vector of 84 features. The output layer receives the 84 features vector and returns a vector of 10 probabilities, the value of each position of the vector represents the probability of that position to be the class that represent the original image that was fed in the input layer.

Beside the convolution and Sub-sampling layers described above, there is another layer in this project call Dropout. The objective of this layer is to avoid overfitting the data in the network by randomly turning off connections between layers.

Parameter Description
EPOCHS Number of training passes
BATCH_SIZE Batch size in training
learning rate Initial rate for the optimizer
Table-2 Model parameters

Additional parameters

Neural networks in general work with weights that are the main parameters of the network – they works as the neuron connections. The objective of the network in this case is to classify which type of cervix is present in an image. A good result in this task depends on how well these weight parameters get tuned by learning.

All parts of the network that were discussed above (convolution layer with activation functions, sub-sampling layers, dropout layers and fully connected layers) are the foundation structure that helps to convey the learning to the network’s weights. The missing piece of this puzzle is the conveyor, which is the technique that iterates through the network, updating the weights, and this is controlled by the parameters listed in the table-5. The conveyor that is used by the ConvNet in this project is well known as AdamOptimizer. It, as well as others optimizers, uses Back-propagation to optimize the values of the weights that better optimize the neural network.

Because the ConvNet needs image data and usually this kind of data consumes a large amount of computational memory, it is necessary to train the network using batches, that means passing a subset of data to the network in the training process. To control the batch sizes, this project uses the parameter Batch Size. For instance if the data contains 8000 images, using a batch size of 64 produces 125 batches in training. The Epoch parameter helps to control how long the training operation will take. For instance, an epoch of 3 and batch size of 64 with 8000 examples of training will cause the optimizer to learn in 375(3*125) batches, for each batch, the network and the optimizer need to digest 64 images to adjust the weights.

Finally, the learning rate is an initial parameter of the optimizer. It is optional because one characteristic of AdamOptimizer is that it automatically initializes and updates this learning rate. However, controlling this parameter by providing an initial value will affect the learning results by controlling how fast or slow the optimizer can converge to discover the weights.

Benchmark

The benchmark model proposed in this project is the LeNet-5 architecture outlined in table-4 with a minor modification in the output layer to predict 3 different classes instead of 10. The benchmark uses the configuration of table-7. According with the metrics defined in Metrics section, the table-8 reports the measurements of the baseline model that will be used to compare with the final model. The data for the baseline model is randomly split in 60% for training 28% and 12% for test.

Parameter Value
EPOCHS 15
BATCH_SIZE 128
learning rate 0.01
Table-3 base model parameters
Metric Value
Train accuracy 0.654
Validation accuracy 0.553
Test Accuracy 0.551
Table-4 Baseline model metrics

III. Methodology

Being able to control the size of the image data when training ConvNet will be useful since it can reduce the amount of computation memory and the training time that the model can take. Also normalizing image data to be zero centered will help the model to converge better.

def resize_image(img, size=(820, 620), debug=False):
    """
    resize image and return it
    """
    h = size[0]
    w = size[1]
    img_ = cv2.resize(img, (w, h))
    return img_

def scale_image(img):
    """
    normalize the image
    """
    return img / 255.0 - 0.5

A function that receives an image and returns it as the model required was implemented to facilitate the image transformation. The code below shows this function named lamba_layer which receives an image, creates a copy, applies the resize function, changes the image color space(in this example this image is being converted from RGB to Gray), and finally scales the image before returning it to the model.

def lambda_layer(image):
    """
    pre-process the image before pass it to the
    ConvNet
    """
    img_ = np.copy(image)
    img_ = resize_image(img_, (H_IMG, W_IMG))
    img_ = cv2.cvtColor(img_, cv2.COLOR_BGR2GRAY)
    img_ = img_[:, :, np.newaxis]
    img_ = scale_image(img_)
    return img_

Implementation

The implementation use Pandas to store the information for the images , OpenCV to read images from file system, scikit-learn as a helper to split the data into training, validation and tests sets, and TensorFlow to implement the ConvNet.

This project use GPU-GRID K520 from AWS with 4GB of memory, however, not all of the data can be fed into the ConvNet because it will cause memory resource exhaustion. For that reason, it was necessary to implement a function generator to lazily generate batches of images that will be passed through the ConvNet. The code below shows how this function is implemented. The function receives a Pandas dataframe that contains images path and type, then maps this input to a randomized set of images that will be preprocessed. Each time this function is called, it will generate a set of images and labels according with the batch size.

def generator(samples,batch_size=128):
    """
    Generates random batches of data base on image path
    """

    num_samples = len(samples)
    while True:
        randomsamples = samples.sample(frac=1)
        for offset in range(0, num_samples, batch_size):
            batch_samples = samples[offset:offset+batch_size]
            
            images = []
            labels = []
            for _, row in batch_samples.iterrows():
                image_path = row['image'].strip()

                image = cv2.imread(image_path)
                label = row['target']

                images.append(lambda_layer(image))
                labels.append(label)

            X_train = np.array(images)
            y_train = np.array(labels)

            yield sklearn.utils.shuffle(X_train, y_train)

The evaluate function performs accuracy operations within a Tensorflow session and returns how well the model accuracy performs.

def evaluate(sess, generator, steps, accuracy_op, dict_opts={}):
    total_examples = 0
    total_accuracy = 0

    for step in range(0, steps):
        batch_x, batch_y = next(generator)
        accuracy = sess.run(accuracy_op, feed_dict={ **{ x: batch_x, y: batch_y }, **dict_opts})
        num_examples = len(batch_x)
        total_accuracy += (accuracy * num_examples)
        total_examples += num_examples
    return total_accuracy / total_examples

The test_model function evaluates a stored model on the test set and reports its accuracy.

def test_model(test_gen, test_steps, accuracy_op, saver, dict_opts={}, name_model="."):
    """
    Test a saved model with test data
    """
    if not os.path.exists(name_model+".index"):
        print(name_model, "Model does not exists in disk")
        return False
    with tf.Session() as sess:
        saver.restore(sess, name_model)
        test_accuracy = evaluate(sess, test_gen, test_steps, accuracy_op, dict_opts=dict_opts )
        print("Test Accuracy = {:.3f}".format(test_accuracy))

The following function with name “training_validation” was created to perform training and validation of the model. The next paragraphs will explain every parameter that this function receive in order to make sense how the model is being trained.

Function “training_validation” parameters:

  • name_model: The name of the model this will be used to store the model in disk and print results

  • train_gen: As explained above this is an initialized generator function with training data

  • val_gen: As explained above this is an initialized generator function with validation data

  • train_steps and val_steps: Number of batches which contains both training and validation sets

  • train_op: Tensorflow operation that minimize the loss function of the model.

  • accuracy_op: Tensorflow operation that calculate the accuracy of the model

  • saver: Object that can be used to store or retrieve a model

  • train_opts: Options that can be passed to the feed dictionary of tensor training operation

  • dict_ops: Options that can be passed to the feed dictionary of tensor for validation or test operations

  • old_train and old_model: To control whether yes or not the training should be on top of a pre trained model

  • store: To control whether yes or not store the final model

  • epochs: Number of epochs the training will perform

The training_validation function stores the model in each epoch such that the model can be retrained from one of the epoch results.

def training_validation(name_model, train_gen, val_gen, train_steps,
                        val_steps, train_op, accuracy_op, saver,
                        train_opts={}, dict_ops={}, old_train=False,
                        old_model='', store=False, epochs=3):
    """
    Train a model, store the model in disk and return the path
    """

    return_data = {
       'save_path': './'+name_model
    }

    with tf.Session() as sess:
        if old_train:
            if not os.path.exists('./'+old_model+".index"):
                print(old_model, "Model does not exists in disk")
                return return_data
            saver.restore(sess, './'+old_model)
        else:
            sess.run(tf.global_variables_initializer())

        print(name_model, "Training...")
        print()

        for i in range(epochs):
            for step in range(0, train_steps):
                batch_x, batch_y = next(train_gen)

                sess.run(train_op, feed_dict={**{x: batch_x, y: batch_y}, **train_opts })
            
            train_accu = evaluate(sess, train_gen, train_steps, accuracy_op, dict_opts=dict_ops)
            val_accu = evaluate(sess, val_gen, val_steps, accuracy_op, dict_opts=dict_ops)

            #Save trainning per epoch
            saver.save(sess, './'+name_model+str(i+1))
            print("EPOCH {} ...".format(i+1))
            print("Train Accuracy = {:.3f}".format(train_accu))
            print("Validation Accuracy = {:.3f}".format(val_accu))
            print()


            
        if store:
            saver.save(sess, return_data['save_path'])
            print(name_model, "Model saved")
        
    return return_data

The LeNet-5 architecture discussed in this project is implemented in the following function using Tensorflow.

def LeNet5(x, init_channels=1, fcx0_len=400):
    mu = 0
    sigma = 0.1
    
    conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, init_channels, 6), mean = mu, stddev = sigma))
    conv1_b = tf.Variable(tf.zeros(6))
    conv1   = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b

    conv1 = tf.nn.relu(conv1)

    conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')

    conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 6, 16), mean = mu, stddev = sigma))
    conv2_b = tf.Variable(tf.zeros(16))
    conv2   = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
    
    conv2 = tf.nn.relu(conv2)

    conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')

    fc0   = flatten(conv2)

    fc1_W = tf.Variable(tf.truncated_normal(shape=(fc0_len, 120), mean = mu, stddev = sigma))
    fc1_b = tf.Variable(tf.zeros(120))
    fc1   = tf.matmul(fc0, fc1_W) + fc1_b
    fc1   = tf.nn.relu(fc1)

    fc2_W  = tf.Variable(tf.truncated_normal(shape=(120, 84), mean = mu, stddev = sigma))
    fc2_b  = tf.Variable(tf.zeros(84))
    fc2    = tf.matmul(fc1, fc2_W) + fc2_b
    
    fc2    = tf.nn.relu(fc2)

    fc3_W  = tf.Variable(tf.truncated_normal(shape=(84, 3), mean = mu, stddev = sigma))
    fc3_b  = tf.Variable(tf.zeros(3))
    logits = tf.matmul(fc2, fc3_W) + fc3_b

    return logits

The hyper parameters were initialized as follow

BATCH_SIZE = 128
H_IMG, W_IMG = (32,32)
EPOCHS = 6
rate = 0.01

The following code shows how the data generators were initialized. Since this project contemplates that a training can start from an older, trained model, the train set, validation set and test set were stored in csv files and are retrieved from these files to be consistent with this data over all training process.

train_samples, validation_samples = train_test_split(data, test_size=0.4)
validation_samples, test_samples  = train_test_split(validation_samples, test_size=0.3)

train_generator = generator(train_samples, batch_size=BATCH_SIZE)
validation_generator = generator(validation_samples, batch_size=BATCH_SIZE)
test_generator = generator(test_samples, batch_size=BATCH_SIZE)

train_steps      = math.ceil(len(train_samples)/BATCH_SIZE)
validation_steps = math.ceil(len(validation_samples)/BATCH_SIZE)
test_steps       = math.ceil(len(test_samples)/BATCH_SIZE)

The Tensorflow operations that use LeNet-5 architecture are shown in the following code:

x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 3)

logits = LeNet5(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=one_hot_y)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate=rate)
training_operation = optimizer.minimize(loss_operation)
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

As discussed above, the function training_validation receives the training_operation and accuracy_operation and the other parameters previously described to train the model.

saver = tf.train.Saver()
lenet_5_data = training_validation('lenet5', train_generator, validation_generator,
                                   train_steps, validation_steps, training_operation,
                                   accuracy_operation, saver, train_opts={}, dict_ops={},
                                   old_train=False, store=True, epochs=EPOCHS)

finally to test the model the next code was used

test_model(test_generator, test_steps, accuracy_operation, saver, dict_opts={}, name_model=lenet_5_data['save_path'])

Refinement

This section explains how the solution model based on LeNet-5 was built by applying modifications to the network in order to increase the performance of evaluation metrics that indicate better results than the benchmark model. Different experiments were performed with combinations of settings specific to the Convolutional Neural Networks, for example, adding or removing filters from convolutions, adding convolution layers, changing the patch size of the convolution, etc. In addition, experimentation with dropout layers and pooling layers are considered in this section to improve model performance.

Experimentation using other color spaces for the images, like RGB, HSV, YCrCb, are considered, as well as the normalization of the images to be zero centered. After experimentation, the best model with best accuracy on training, validation and test sets will be chosen as finally solution model.

The first model solution was based on LeNet-5 described in Algorithms and Techniques section, table-5 shows the architecture and table-6 the results of this architecture.

Layer name Size Channels
Input 155x155 3
Convolution 1 (C1) 151x151 6
Sub-sampling 75x75 6
Convolution 2 (C2) 71x71 16
Sub-sampling 35x35 16
Fully connect (FC1) 120 -
Fully connect (FC2) 84 -
Output 3 -
Table-5 LeNet-5

The ConvNet outlined in table-9 was trained using the following parameters using different color spaces and obtaining the results that shows table-10

Parameters:

  • EPOCHS = 10
  • learning rate = 0.01
Color Space Train Validation Test
RGB 3 channels 0.335 0.336 0.320
HSV 3 channels 0.766 0.514 0.523
YCrCb 3 channels 0.748 0.504 0.483
Table-6 Report first solution

As table-6 shows, the best model in the first solution is the one that use HSV Color Space. Since this first solution model does not show big improvements based on the benchmark model, the next steps of improvement were to decrease the learning rate, increase number of epochs and add neurons in fully connected layers FC1 from 120 to 1000 and FC2 from 84 to 250 neurons.

The table-7 shows the results of the model evaluated in the three color spaces. The model with YCrCb color space performs better that the other two, however it shows signs of overfitting.

Parameters:

  • EPOCHS = 10
  • learning rate = 0.0008
Color Space Train Validation Test
RGB 3 channels 0.997 0.641 0.619
HSV 3 channels 0.979 0.648 0.630
YCrCb 3 channels 0.985 0.646 0.623
Table-7 Report solution first improvement

The next improvement was to add dropout layers next to the fully connected layers FC1 and FC2 with value of (0.5) and increased number of epochs to 20. The results are shown in Table-8. This experiment results still suffers of overfitting despite the dropout layers.

Parameters:

  • EPOCHS = 20
  • learning rate = 0.0008
Color Space Train Validation Test
RGB 3 channels 0.997 0.648 0.620
HSV 3 channels 0.999 0.660 0.663
YCrCb 3 channels 0.997 0.654 0.641
Table-8 Report solution second improvement

Other experiments that were performed are shown in table-9, the intention was to explore different channels of color spaces and some combinations looking for decrease the overfitting. The kernel sizes of the pooling layers will be increased. Only HSV and YCrCb color spaces are considering for this experiment Table-9 shows the results.

Parameters:

  • EPOCHS = 20
  • learning rate = 0.0008
Color Space Train Validation Test
HSV(Hue) 0.912 0.626 0.624
HSV(Saturation) 0.960 0.672 0.656
HSV(H+S) 0.954 0.676 0.658
HSV(S+B) 0.970 0.683 0.637
YCrCb(Y) 0.976 0.648 0.639
YCrCb(Cr) 0.925 0.670 0.630
YCrCb(Cb) 0.924 0.668 0.661
YCrCb(Y+Cr) 0.921 0.658 0.615
YCrCb(Cr+Cb) 0.946 0.686 0.665
Table-9

The results above indicate that the best model, according to the validation and test scores, is the one that uses HSV color space with H+S channels. All of the experimented models show strong signs of overfitting despite the effort to reduce it. In order to improve on the selected model, five re-trainings with 20 epochs each were performed, keeping the learned weights of the previous trainings. However, the results were not different and the overfitting remained the same.

This project considered to continue the evaluation of this model despite the overfitting due to time restriction. The model architecture obtained after perform the experiments is outlined in Table-10.

Layer name Size Channels
Input 155x155 3
Convolution 1 (C1) 149x149 6
Sub-sampling 73x73 6
Convolution 2 (C2) 69x69 16
Sub-sampling 32x32 16
Fully connect (FC1) 1000 -
Dropout(0.5) - -
Fully connect (FC2) 250 -
Dropout(0.5) - -
Output 3 -
Table-10 Model architecture HSV (H+S)

Since the first solution based on LeNet 5 did not bring the expected results, another approach call transfer learning using ConvNet architecture AlexNet [7] was used as an improvement. AlexNet is a pre-trained neural network that contains 60 million parameters and 650,000 neurons.

The architecture of AlexNet is shown in Figure-8, it has five convolution layers, some max-pooling layers and three fully connected layers. This network was trained to classify 1.2 million images that can fall down into one of one thousand different categories.

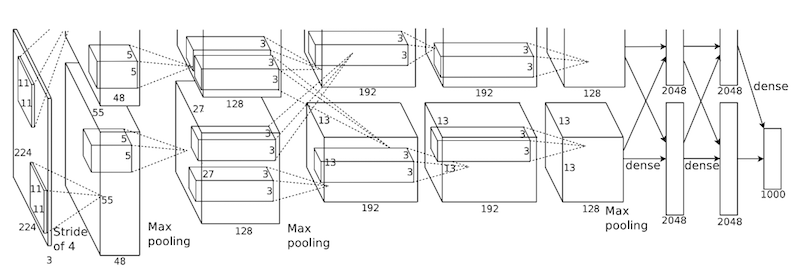alt text Figure-8 Source: AlexNet [7]

For this experiment the pre-trained AlexNet model was used with its convolution and two fully connected layers, the fully connected layers and output layers from the previous model LetNet-5 were appended to the last fully connected layer of AlexNet. The Table-11 shows the architecture of the new model.

Layer name Size Channels
Input 155x155 3
AlexNet Pretrained 4096 -
Fully connect (FC1) 1000 -
Dropout(0.5) - -
Fully connect (FC2) 250 -
Output 3 -
Table-11 AlexNet pretrained model

With the model outlined above, several experiments were performed using the same color space as other experiments namely RGB, HSV and YCrCb. AlexNet performs better with RGB and the parameters above were used to obtain results of Table-12

Parameters:

  • EPOCHS = 100
  • learning rate = 0.0008
  • Color Space RGB
Metrics Value
Train 0.959
Validation 0.697
Test 0.659
Table-12 Report solution AlexNet

Reflection

Reaching a final solution was a process that took a long time of experimentation with different settings to try to overcome the overfitting of data.

The process can be summarized in the following steps:

Data Exploration

The data was downloaded from Kaggle, uncompressed and analyzed. I found that it was necessary to normalize the image sizes to be consistent with the input of the model that will process it. During the process, different color space were explored and then applied to the model.

In the exploration imaging tools like ImageMagick were applied to the image files to detect corrupt data and a few samples were found

Data Modeling

At the beginning, it was clear that applying Convolutional Neural Network to images classification problem is probably a good fit to find out a good solution. This project started out on LeNet-5 Architecture, a well known Convolutional Neural Network that has gotten good results of different images classifications like digit classifier and traffic sign predictions among others.

Model Experimentation

This process took more time than others since different settings and combination of parameters were performed to pursue the desired results.

Different assumptions were made in this step, such as including different color spaces in the experiments to see if there are some channels that can better be consumed by the ConvNet and get betters results.

Changing the architecture of the ConvNet and adjusting hyper parameters with the aim of better accuracies were performed in this step.

Model Refinement

This is an extension of model experimentation that were performed by revisiting the results of the experiments, looking for hints that lead to extra parameters or architecture tuning.

Evaluation

The evaluation was performed through the experimentation process after every training the test set were used to evaluate the model.

A better, final solution, despite all of the efforts to reach a very good model that does not overfit the test set, was not possible.

Improvement

There are several improvements that were considered in this project but were not explored due to scope of time or missing knowledge to integrate on this solution.

More image preprocessing

Considering this data set are images from cervix an improvement would be to have some preprocessing techniques to find regions of interest within these images and to discard the noise elements present on the images, like metal tools.

Applying more complex ConvNet Architectures

During the process I tried to use pre-trained AlexNet architecture, having almost near results to the LetNet model; however, trying even more complex architectures like VGG-16 or ResNet could bring better results.

Getting more data

One aspect of this project is that data is not enough to build a robust model, obtaining more data for analysis with more complex methods, like applying clustering or mixture models to get more insights of data variety, will be a very good option to explore. However getting data about cervix screening was difficult.

I’m sure having more time to study and apply the improvements above can lead to a better and more robust solution.

Thanks to Udacity Team and David Edelsohn for their insights and feedback

References

  1. Yann Lecun, “LeNet-5, convolutional neural networks”, http://yann.lecun.com/exdb/lenet/

  2. Data Augmentation Tool, https://github.com/codebox/image_augmentor

  3. AlexNet architecture, https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf